Instructions
How to Determine What Torque You Need for Your Servo Motors
When building a robotic system with servo motors, determining the appropriate torque for each motor is essential. Torque is what allows the servo motor to effectively lift, hold, or move an object. Without sufficient torque, your motor either won’t perform as expected or may damage itself trying.
Here, we’ll break down how to calculate the torque you need, then pivot into some key nuances around how torque works in different contexts.
What Is Torque?
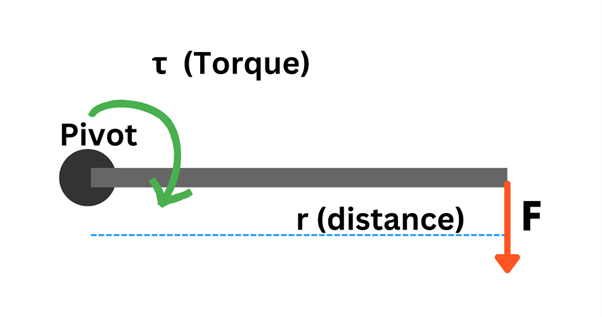
Torque is a force applied over a distance that causes rotation. You use torque every day when you twist open a jar or turn a doorknob. In the case of servo motors—specifically in robotics—torque determines how much weight a motor can rotate at a certain distance away from its axis. Think about a robotic arm lifting a heavy object: the motor's torque directly affects how much weight the arm can lift, and at what speed.
Mathematically, torque is expressed as:
τ = r × F
- τ is torque,
- r is the distance from the axis of rotation,
- F is the force applied.
If that feels abstract, consider that F is usually the force caused by gravity, meaning it depends on the weight of the object and its distance from the motor's center.
Torque and Servo Motors: The Core Relationship
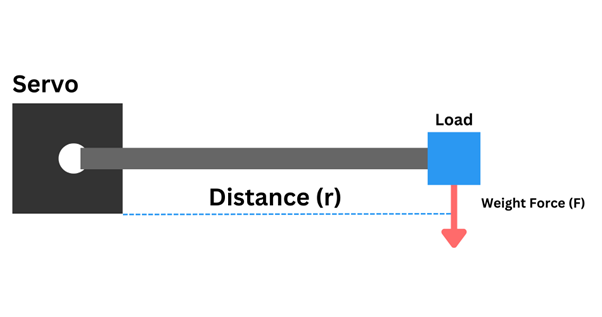
Servo motors are frequently used in robotic arms or other machines with rotational mechanisms. The amount of torque a servo motor can exert determines its capability to perform mechanical tasks, especially when dealing with varying loads.
The lever arm length—the distance from the rotation point to the load—amplifies the effect of the weight being moved. A longer lever arm requires more torque even if the weight remains the same. So, as we dive into calculations, remember that torque isn't just about force; it’s also about how far away from the motor's axis that force is applied.
Formula Recap
The standard torque equation for servo motors typically used in applications like robotic arms can be expanded slightly:
τ = r × m × g
- r is the distance from the motor's axis to where the load is applied,
- m is the mass of the item being moved (in kilograms),
- g is the acceleration of gravity (~9.81 m/s²).
Let’s translate this into something more immediately practical: a robotic arm needs torque to lift an object at the end of the arm. If the arm is long, you’ll need more torque to achieve that same lift, even if the object you’re lifting doesn’t change in weight.
Components of Torque in Servo Motors
1. Weight of Components
The force caused by the weight of objects being moved is simple physics. Every load you expect the motor to handle has a weight. Multiplied by gravity, that’s your F.
A robotic arm lifting a box must overcome the weight of the box. However, the motor also needs to account for the weight of the components themselves, like robotic arm links or grippers.
2. Distance from the Pivot
The lever arm length is just as crucial. Calculating torque by only considering force and weight without factoring in the arm’s length will result in inaccurate torque requirements and potentially a poor design.
Case Study: A Simple Robotic Arm
Imagine an arm that needs to lift a 1.5 kg box at the end of a 0.5-meter-long arm.
- m = 1.5 kg
- r = 0.5 m
- g = 9.81 m/s² (constant)
We’re now ready to plug in values:
τ = r × m × g
τ = 0.5 m × 1.5 kg × 9.81 m/s²
τ = 7.36 Nm
This means you require a minimum torque of 7.36 Newton-meters (Nm) to lift the box at the end of this particular robotic arm.
Angular Acceleration
In any instance where you need the servo motor to move a load and not just hold it, you must also account for angular acceleration. Angular acceleration means your motor needs extra torque at the beginning and during changes in movement. To calculate it:
τ = I × α
- I is the moment of inertia of the robot arm (resistance to angular motion),
- α is angular acceleration.
This means that for movements such as high-speed rotations or rapid direction changes, torque requirements jump. The speed with which the load moves and how quickly the direction changes are factored into torque calculations for dynamic motion.
Final Thoughts
To summarize everything, calculating torque isn’t just as simple as deciding how heavy a load is. It requires you to think about:
- Distance (where the weight is applied from the axis),
- Weight of the object being moved,
- The weight of other mechanical components (like links and joints inside the machine),
- Angular acceleration, especially if the motor will be moving or changing directions rapidly,
- Safety margins (plan a buffer of 20-30% torque capability beyond the minimum).
The general idea is that the larger the load or the further away from the pivot, the more torque you need. By thinking through all of these details, you can properly size your servo motor torque needs, ensuring your motor will handle everything smoothly without underperformance during operation.
Get expert servo motor guidance and competitive pricing from Wake Industrial. Whether you need one motor or a complete system, we'll help you find the right solution at the right price. Call 1-919-443-0207 now for a quick quote or email sales@wakeindustrial.com to browse our extensive servo motor inventory.
Instructions
How to Determine What Torque You Need for Your Servo Motors
When building a robotic system with servo motors, determining the appropriate torque for each motor is essential. Torque is what allows the servo motor to effectively lift, hold, or move an object. Without sufficient torque, your motor either won’t perform as expected or may damage itself trying.
Here, we’ll break down how to calculate the torque you need, then pivot into some key nuances around how torque works in different contexts.
What Is Torque?

Torque is a force applied over a distance that causes rotation. You use torque every day when you twist open a jar or turn a doorknob. In the case of servo motors—specifically in robotics—torque determines how much weight a motor can rotate at a certain distance away from its axis. Think about a robotic arm lifting a heavy object: the motor's torque directly affects how much weight the arm can lift, and at what speed.
Mathematically, torque is expressed as:
τ = r × F
- τ is torque,
- r is the distance from the axis of rotation,
- F is the force applied.
If that feels abstract, consider that F is usually the force caused by gravity, meaning it depends on the weight of the object and its distance from the motor's center.
Torque and Servo Motors: The Core Relationship

Servo motors are frequently used in robotic arms or other machines with rotational mechanisms. The amount of torque a servo motor can exert determines its capability to perform mechanical tasks, especially when dealing with varying loads.
The lever arm length—the distance from the rotation point to the load—amplifies the effect of the weight being moved. A longer lever arm requires more torque even if the weight remains the same. So, as we dive into calculations, remember that torque isn't just about force; it’s also about how far away from the motor's axis that force is applied.
Formula Recap
The standard torque equation for servo motors typically used in applications like robotic arms can be expanded slightly:
τ = r × m × g
- r is the distance from the motor's axis to where the load is applied,
- m is the mass of the item being moved (in kilograms),
- g is the acceleration of gravity (~9.81 m/s²).
Let’s translate this into something more immediately practical: a robotic arm needs torque to lift an object at the end of the arm. If the arm is long, you’ll need more torque to achieve that same lift, even if the object you’re lifting doesn’t change in weight.
Components of Torque in Servo Motors
1. Weight of Components
The force caused by the weight of objects being moved is simple physics. Every load you expect the motor to handle has a weight. Multiplied by gravity, that’s your F.
A robotic arm lifting a box must overcome the weight of the box. However, the motor also needs to account for the weight of the components themselves, like robotic arm links or grippers.
2. Distance from the Pivot
The lever arm length is just as crucial. Calculating torque by only considering force and weight without factoring in the arm’s length will result in inaccurate torque requirements and potentially a poor design.
Case Study: A Simple Robotic Arm
Imagine an arm that needs to lift a 1.5 kg box at the end of a 0.5-meter-long arm.
- m = 1.5 kg
- r = 0.5 m
- g = 9.81 m/s² (constant)
We’re now ready to plug in values:
τ = r × m × g
τ = 0.5 m × 1.5 kg × 9.81 m/s²
τ = 7.36 Nm
This means you require a minimum torque of 7.36 Newton-meters (Nm) to lift the box at the end of this particular robotic arm.
Angular Acceleration
In any instance where you need the servo motor to move a load and not just hold it, you must also account for angular acceleration. Angular acceleration means your motor needs extra torque at the beginning and during changes in movement. To calculate it:
τ = I × α
- I is the moment of inertia of the robot arm (resistance to angular motion),
- α is angular acceleration.
This means that for movements such as high-speed rotations or rapid direction changes, torque requirements jump. The speed with which the load moves and how quickly the direction changes are factored into torque calculations for dynamic motion.
Final Thoughts
To summarize everything, calculating torque isn’t just as simple as deciding how heavy a load is. It requires you to think about:
- Distance (where the weight is applied from the axis),
- Weight of the object being moved,
- The weight of other mechanical components (like links and joints inside the machine),
- Angular acceleration, especially if the motor will be moving or changing directions rapidly,
- Safety margins (plan a buffer of 20-30% torque capability beyond the minimum).
The general idea is that the larger the load or the further away from the pivot, the more torque you need. By thinking through all of these details, you can properly size your servo motor torque needs, ensuring your motor will handle everything smoothly without underperformance during operation.
Get expert servo motor guidance and competitive pricing from Wake Industrial. Whether you need one motor or a complete system, we'll help you find the right solution at the right price. Call 1-919-443-0207 now for a quick quote or email sales@wakeindustrial.com to browse our extensive servo motor inventory.